Tutorial: Efficient runtime patching of models with PyGlove
For most machine learning developers, creating neural network models is a constant flow of experimenting new layers, normalization techniques, learning rate schedulers, and more. Even a minor variation like the initialization scheme can provide valuable accuracy gains in the downstream pipeline. However, adapting and customizing outside code to your own codebase takes time and limits the amount of ideas that can tested in a short timeframe, even when such code is available online.
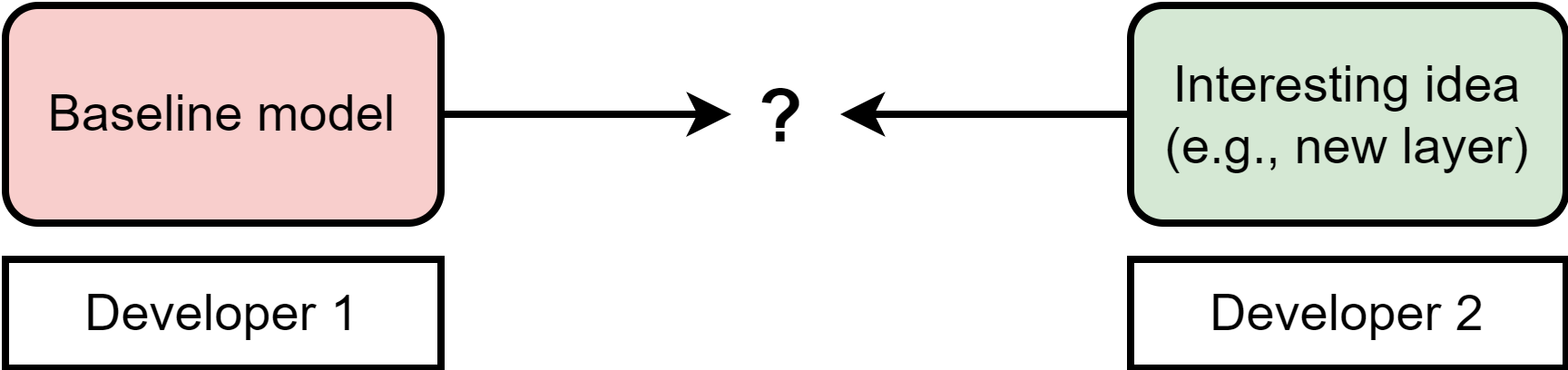
PyGlove is a Python library developed to simplify the runtime manipulation of models by two core ideas: working on “symbolic objects” and manipulating them via “patches”.1 2 A symbolic object is a wrap of the original object (e.g., a neural model) that remembers its initialization arguments and routines. This effectively creates a tree-like structure that can be traversed and manipulated with an abstract logic. How to apply new components is described as a series of node manipulations on the tree (“patching”). A patch can be applied by external users automatically, thus limiting unecessary friction.
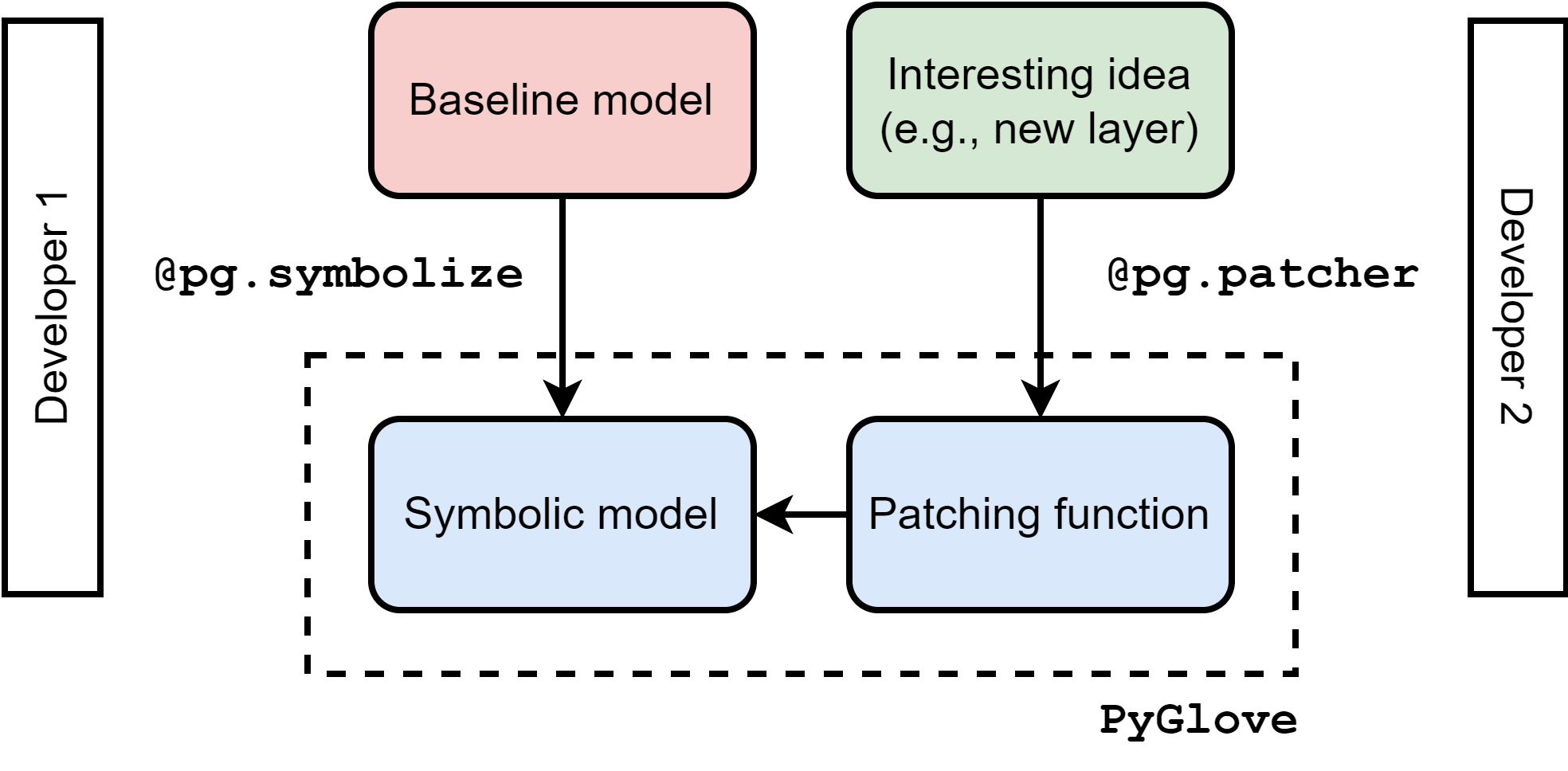
PyGlove was originally developed for increasing collaboration in teams, but its use case is interesting also for small research groups.1 This blog post is a short tutorial I wrote based on my initial experiments with the library. It is not supposed to be as comprehensive as the official documentation, and the examples might not be the optimal way to achieve the intended effects. Still, I think it provides an interesting glimpse into the main ideas and on whether the library can be useful. I cover briefly how to turn a model into a symbolic object (part 1), how to define traversal functions (part 2), and how to write generic patches (part 3).
🔗 The code for this tutorial is available as a notebook. At the moment of writing, PyGlove is at version 0.2.1:
pip install pyglove==0.2.1 --quiet
Introduction: symbolic programming
To understand the need for PyGlove, consider a simple MLP network with a single output, written in PyTorch:
def build_model(in_channels, hidden_channels):
return nn.Sequential(
nn.Linear(in_channels, hidden_channels),
nn.ReLU(),
nn.Linear(hidden_channels, 1)
)
Even on this simplistic model, there are many ideas that could be tested: modifying the activation function, changing the initialization, adding dropout, etc. Each modification requires us to rewrite build_model to make it more parametric. However, in some cases the best way to add a new component might be non-trivial (e.g., what is a good default probability for dropout? should we add it before or after each activation function?). This creates friction between people who are designing new components and people who want to experiment with them. Worse, sometimes we may not have writing access to the original code and we can only manipulate runtime instances of the model.
PyGlove is predicated around the idea of symbolic objects. Informally, these are like standard objects, but they keep a reference to the parameters that were used to initialize them (image taken from the documentation):
There are several ways to build a symbolic object, but the simplest one is the symbolize decorator, which can be used to decorate existing classes or even runtime instances:
import pyglove as pg
Linear, ReLU, Sequential = pg.symbolize(nn.Linear), pg.symbolize(nn.ReLU), pg.symbolize(nn.Sequential)
PyGlove provides tools to perform automatic data validation on the initialization parameters; we provide a simple example towards the end.
Now that we have the symbolic layers, we replace the original layers with the symbolic ones in the model definition:
def build_model(in_channels, hidden_channels):
return Sequential(
Linear(in_channels, hidden_channels),
nn.ReLU(),
Linear(hidden_channels, 1)
)
We can appreciate the differences by printing out an instance of the new symbolic object using its specialized format function:
mlp = build_model(4, 8)
print(mlp.format(hide_default_values=True))
>> Sequential(
args = [
0 : Linear(
in_features = 4,
out_features = 8
),
1 : ReLU(),
2 : Linear(
in_features = 8,
out_features = 1
)
]
)
Each symbolic object (e.g., Sequential) has a memory of its initialization arguments. Because some of them are symbolic objects themselves (e.g., the ReLU object), this creates a tree-like structure describing the object, similar to JAX’s pytrees.
PyGlove has a number of useful functions to traverse this tree. Each node of the tree is described by a key (a unique identifier), its value, and the value of its parent object. The key is a simple URI-like path that has the same format as a nested property in pure Python:
# k: key, v: value, p: parent
pg.traverse(mlp, lambda k,v,p: print(k))
>> args
args[0]
args[0].in_features
args[0].out_features
args[0].bias
args[0].device
args[0].dtype
args[1]
args[1].inplace
args[2]
args[2].in_features
args[2].out_features
args[2].bias
args[2].device
args[2].dtype
True
We can query the model to extract all subportions that satisfy certain properties, e.g., all linear layers:
pg.query(mlp, where=lambda v: isinstance(v, Linear))
>> {'args[0]': Linear(in_features=4, out_features=8, bias=True, device=None, dtype=None),
'args[2]': Linear(in_features=8, out_features=1, bias=True, device=None, dtype=None)}
Queries and traversals can also be constrained on keys through a regular expression. This, combined, with queries like the one above, allows a developer to easily write sophisticated routines to inspect models.
Dynamic rebinding on symbolic objects
Symbolic objects are useful because we can dynamically manipulate their properties while maintaning internal consistency. The simplest way to achieve this is by rebinding one property, such as the number of input features:
mlp2 = mlp.clone()
mlp2 = mlp2.rebind({'args[0].in_features': 10})
We can print the difference between the two models with a diff operation:
print(pg.diff(mlp, mlp2))
>> Sequential(
args = [
0 = Linear(
in_features = Diff(
left = 4,
right = 10
)
)
]
)
PyGlove has automatically re-initialized the first linear layer of the model with the new requested shape. Note that this mechanism may fail: for example, if we modify args[0].out_features (the hidden size), we should reinitialize both linear layers to maintain consistency. In this case, PyGlove provides an event-based API that is triggered everytime a property is rebound.
In general, I have found that rewriting models and trainers to conform to PyGlove’s constraints can be harder than advertised. For example, symbolic nodes are constructed by the initialization parameters, which works for a sequential object, but fails for a generic subclassed model (see my issue here). I have not found efficient workarounds for this scenario at the moment.
Model patching with symbolic rules
Modifying a symbolic object at runtime provides a new level of flexibility to developers, with the possibility to define transformations on trees that are reminiscent of higher-order transformations of pytrees in JAX. PyGlove calls these transformations patches. In the simplest case, a patch provides a dictionary of values to rebind. For example, we can patchify the previous rebind as follows:
@pg.patcher([])
def prelu_activation(mlp):
return {'args[1]': nn.PReLU()}
A patch can be instantiated as a function or from a URI-like path (in order to use patches directly from the command line):
patch = prelu_activation()
# Equivalent
# patch = pg.patching.from_uri('prelu_activation')
print(pg.patch(mlp, patch))
>> Sequential(
args = [
0 : Linear( ... ),
1 : PReLU(num_parameters=1),
2 : Linear( ... )
]
)
In a more interesting case, patches can provide a callable acting on a generic key/value/parent triplet, similar to the traversal operation from before. For example, here is a simple patch to add dropout before each dense layer:
@pg.patcher([
('prob', pg.typing.Float(min_value=0.0, max_value=1.0))
])
def add_dropout_before_linear(mlp, prob):
def _add_dropout(k, v, p):
if isinstance(v, Linear):
return Sequential(Dropout(prob), v)
return v
return _add_dropout
This patch is parametric, and the decorator allows us to specify several input validation constraints via the typing submodule. Note that the patch below can be written with little knowledge of the downstream model, i.e., from the person developing the original dropout layer in this case. All patches are automatically registered by PyGlove, and they can be combined:
pg.patching.patcher_names()
>> ['prelu_activation', 'add_dropout_before_linear']
print(pg.patch(mlp,
[prelu_activation(),
add_dropout_before_linear(prob=0.2)]
)
)
Ideally, patches should decouple the work of defining how to apply a new component to a model from the developers that want to experiment with them. The way this is argued in the paper is that, with $n$ models and $m$ patches, we need work in the order of $nm$ without PyGlove (each combination of model and patch) and only $n+m$ with it (reproduced from 2):
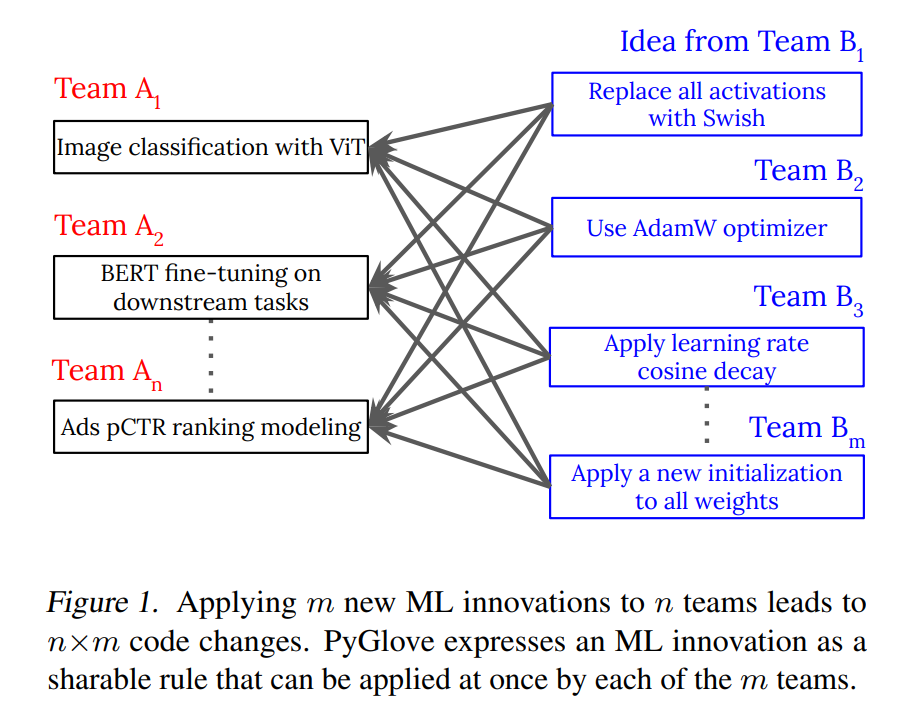
Of course, real world patches should probably consider a wide range of edge cases to work reasonably, but the main idea still stands.
Conclusions
PyGlove has a few additional components that I did not consider in detail. For example, it is easy to describe families of models by replacing an input with a collection of symbols or a generic search space:
mlps = Sequential(
Linear(5, 10),
pg.one_of([nn.ReLU(), nn.PReLU()]),
Linear(10, 1)
)
This in turn can potentially automate model optimization or experiment management. In general, I find the idea behind the library very promising, but customizing our own code to fit into the constraints of symbolic objects may not be trivial or immediate. Whether this is advantageous depends on you and your team, but I will definitely follow with interest the future evolutions of the library.
Follow me on Twitter for almost daily updates.
References
-
Peng, D., et al., 2020. PyGlove: Symbolic programming for automated machine learning, NeurIPS 2020. ↩ ↩2
-
Peng, D., et al., 2023. PyGlove: Efficiently Exchanging ML Ideas as Code. arXiv preprint arXiv:2302.01918. ↩ ↩2